Poussée, accélération, G et RPP

Si vous avez déjà recherché quelques informations relatives aux fusées, il y a fort à parier que vous ayant entendu les termes de G et RPP (ou TWR pour les anglophones). Ces concepts peuvent sembler déroutants au premier abord mais nous allons voir ensemble qu’ils ne cachent rien de bien compliqué.

Dans cet article, nous allons présenter ces concepts en étudiant le décollage d’une fusée.

La poussée d’une fusée

Une fusée avance en expulsant du gaz à l’opposé de son sens de direction : si elle doit aller vers le haut, alors elle expulse du gaz vers le bas. Vous pouvez faire une expérience similaire chez vous avec un simple ballon de baudruche : gonflez le ballon et maintenez-le fermé avec l’ouverture vers le bas. Lorsque vous relâchez l’ouverture, l’air à l’intérieur du ballon est poussé vers le bas et le ballon est alors poussé vers le haut. C’est le principe énoncé par la 3^ème loi de Newton.¹

Si le gaz va vers le bas, c’est parce qu’un force le pousse dans cette direction. D’après la 3^ème loi de Newton, cela veut dire qu’une force égale et pousse le ballon dans la direction opposée. Dans le cas d’une fusée, les moteurs poussent du gaz vers le bas avec une certaine force : c’est cette force que l’on appelle la poussée d’une fusée.²³⁴ Comme la poussée est une force, son unité dans le système international est le Newton, noté N.⁵

De la poussée à l’accélération

On a vu que c’est la poussée fournie par les moteurs qui permet à une fusée d’avancer. Mais ce que l’on veut, c’est savoir à quelle vitesse elle va pouvoir décoller. Et c’est là qu’il ne faut pas confondre un lancer de balle et le fonctionnement d’une fusée : ce qui permet de prédire le mouvement de la balle après le lancement, c’est la vitesse à laquelle elle quitte la main alors qu’une fusée pousse encore après avoir décollé. On ne va donc pas s’intéresser à la vitesse de la fusée mais à son accélération. Et là, on va encore profiter du travail d’Isaac Newton, et en particulier de la deuxième loi de Newton qui a donné la version moderne du principe fondamental de la dynamique : l’accélération d’un objet est proportionnelle à la somme des forces s’exerçant sur lui et inversement proportionnelle à sa masse. En formule mathématique, cela donne :

$$
\vec{a} = \frac{1}{m} \sum_i \vec{F}_i
$$

Où $\vec{a}$ est l’accélération de la fusée, $m$ est sa masse et pour tout $i$, $\vec{F}_i$ est une force s’appliquant sur la fusée.

On va maintenant se placer juste au moment où notre fusée décolle du pas de tir, c’est-à-dire juste après avoir quitté le contact avec le sol. À cet instant, deux forces principales s’appliquent sur la fusée⁶ : le poids de la fusée et sa poussée. On fait l’hypothèse que la fusée est parfaitement à la verticale donc le poids et la poussée son de même direction mais de sens opposé. On peut donc ne s’intéresser qu’à la composante verticale de l’accélération :

$$
a = \frac{1}{m} \left( F_p – m g \right)
$$

Où $m$ est la masse de la fusée, $a$ est son accélération vers le haut, $F_p$ est la poussée vers le haut et $g$ est la pesanteur terrestre. On peut aussi réécrire l’équation pour obtenir la forme suivante :
\begin{equation}
a = g \left(\frac{F_p}{m g} – 1 \right)
\tag{AccG}\label{eq:acc_twr}
\end{equation}
Puisque l’on veut faire décoller la fusée, il faut que l’accélération $a$ soit strictement positive, donc que la poussée $F_p$ soit strictement supérieure au poids $m g$, c’est-à-dire que leur rapport soit strictement supérieur à $1$ :
$$
\frac{F_p}{m g} \gt 1
$$

Le RPP et le nombre de G

Vous avez vu ce nouveau terme que l’on compare à la valeur 1 ? C’est le rapport de la poussée sur le poids de la fusée. On va donc l’appeler rapport poussée sur poids⁷ et on l’abrège souvent RPP.⁸ Ce qui est intéressant, c’est que l’on peut maintenant comparer les accélérations des fusées indépendamment de leur poids : si une fusée a un RPP deux fois plus élevé que celui d’une seconde, alors la première accélérera deux fois plus vite.

Et si on regarde en détail l’équation \eqref{eq:acc_twr}, on remarque que l’accélération de la fusée au niveau de la mer est égale à $g$ fois le RPP moins $1$. Ce dernier terme est présent parce que l’on s’est intéressé à la fusée au niveau de la mer mais si elle est perdue dans l’espace, loin de toute attraction gravitationnelle (en apesanteur), alors l’accélération serait simplement égale au RPP fois $g$. Pour une fusée qui a un RPP égal à $2$, on dira donc que la fusée a une accélération de $2 g$.

On peut remarquer qu’un RPP de $1$ ne permet pas de faire s’élever la fusée du niveau de la mer. Mais s’il n’y avait pas de sol, elle ne tomberait pas non plus : elle est en parfait équilibre. Du point de vue des passagers, le fait que la fusée ait un RPP de $1$ est équivalent à être à la surface de la Terre. Et ce, peu importe que la fusée soit ou non à proximité de la Terre !⁹

Cela veut aussi dire que si le RPP est de $2$, les passagers auront l’impression de peser deux fois plus lourd. Et ce n’est pas qu’une impression : les structures mécaniques de tous les équipements devront également pouvoir supporter ce « poids apparent » supérieur à la normale. On a donc souvent envie de limiter ces efforts mécaniques supplémentaires en limitant le RPP des véhicules spatiaux. Pour ce faire, il faut s’assurer qu’à tout instant du vol, le RPP (défini comme le rapport de la poussée par le poids qui serait ressenti au niveau de la mer sur Terre) soit inférieur à un certain seuil dépendant du contenu du véhicule.

Une petite application ?

Prenons un petit véhicule très simple avec une capsule de commande MK1-3, un parachute Mk16-XL, un découpleur TD-25, un réservoir Rockomax X200-16 et un moteur RE-I5 Skipper. À tout cela vont s’ajouter les trois kerbonautes qui embarqueront dans la capsule de commande avec tout le équipement. On va essayer de calculer le RPP au moment du décollage puis le RPP maximum théoriquement atteignable par le vaisseau. C’est parti !

Les paramètres

Avant de se lancer dans les calculs, commençons par regarder ce qu’il va nous falloir pour calculer ce fameux RPP. Par définition, il va nous falloir récupérer la force de poussée du moteur et le poids du vaisseau.

Pour la force de poussée, elle nous est donnée par le jeu ou par le Wiki disponible en ligne. On apprend donc que le moteur a une poussée de $568.75\ \mathrm{kN}$ dans une atmosphère de pression $1\ \mathrm{atm}$ (lire « une atmosphère »), ce qui correspond à l’atmosphère au niveau de la mer sur Terre ou Kerbin. On apprend également que sa poussée est de $650\ \mathrm{kN}$ dans le vide. La plupart des moteurs de fusée ont cette propriété : ils sont plus efficaces dans le vide que dans une atmosphère mais on en discutera une autre fois.

Pour le poids du vaisseau, on va uniquement considérer l’accélération gravitationnelle au niveau de la mer de Kerbin $g = 9.81\ \mathrm{m/s^{2}}$. Il nous reste à déterminer la masse du vaisseau. On pourrait faire la somme des masses des différentes pièces de notre fusée sans oublier la masse des kerbonautes mais on va plus simplement regarder la masse indiquée dans le bâtiment d’assemblage véhiculaire (BAV ou VAB en anglais) avec le réservoir plein et avoir le réservoir vide :

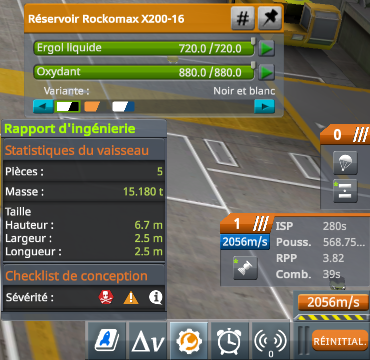
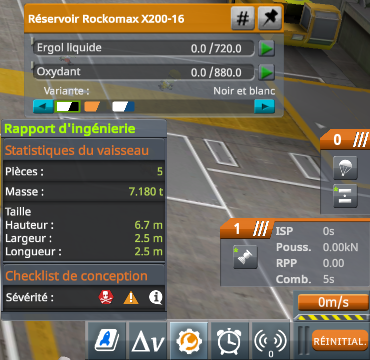
On lit donc que la fusée a une masse de $15.180\ \mathrm{t}$ ou $15 180\ \mathrm{kg}$ lorsque le réservoir est plein et une masse de $7.180\ \mathrm{t}$ ou $7 180\ \mathrm{kg}$ lorsque le réservoir est vide. On a donc maintenant tout ce qu’il nous faut pour attaquer les calculs !

Les calculs

Commençons par calculer le RPP minimal de la fusée lorsque le moteur est à pleine puissance. Puisque le RPP est défini par le rapport de la poussée par le poids, il est minimal lorsque la poussée est la plus baisse et le poids est le plus élevé, c’est-à-dire la masse la plus élevée. Cela se produit donc avec une poussée de $568.75\ \mathrm{kN} = 568 750\ \mathrm{N}$ et une masse de $15 180\ \mathrm{kg}$. On obtient donc :
$$
\mathrm{RPP_{min}} = \frac{568 750}{15 180 \cdot 9.81} \approx 3.819
$$

On peut d’ailleurs vérifier que le BAV nous indique un RPP de $3.82$, ce qui est l’arrondi de la valeur que l’on a trouvée.

C’est donc au tour du RPP maximal qui est atteint lorsque la poussée est maximale et la masse minimale. Cela se produit donc avec une poussée de $650\ \mathrm{kN} = 650 000\ \mathrm{N}$ et une masse de $7 180\ \mathrm{kg}$. On obtient donc :
$$
\mathrm{RPP_{max}} = \frac{650 000}{7 180 \cdot 9.81} \approx 9.228
$$

Comme tout à l’heure, on peut vérifier que le BAV nous indique un RPP de $9.23$ lorsque le réservoir est presque vide et que le moteur pousse comme dans le vide.

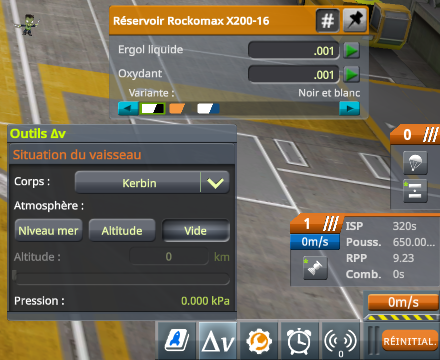
On peut d’ailleurs faire l’expérience : sur le pas de tir, on voit que le RPP indiqué est de $3.83$ alors qu’il atteint $9.15$ lorsque le réservoir est presque vide. Les différences peuvent s’expliquer très simplement.

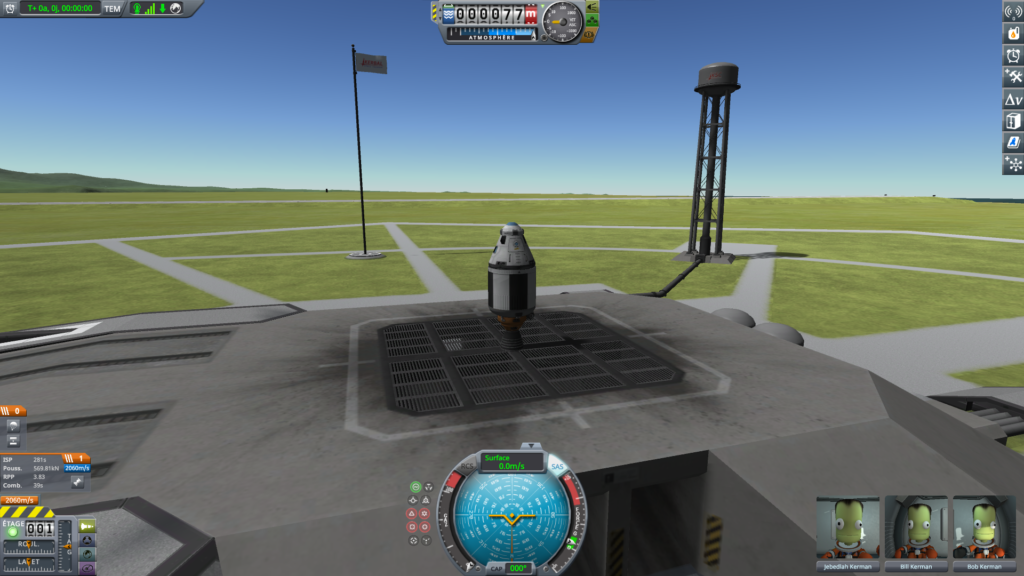
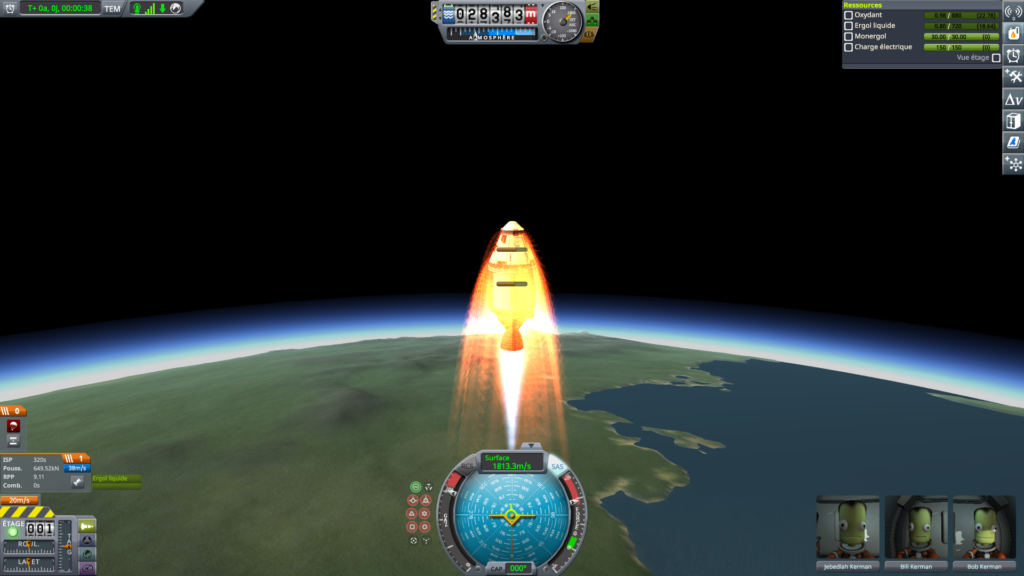
On voit que sur le pas de tir, le moteur a un ISP¹⁰ de $281\ \mathrm{s}$ alors que le Wiki nous indique un ISP au niveau de la mer égal à $280$. On en déduit que le moteur sur le pas de tir a une poussée légèrement supérieure à $568.75\ \mathrm{kN}$.

Le RPP maximal théorique ne semble pas être atteint alors que l’ISP indiqué l’est. C’est tout simplement parce que le réservoir n’est pas encore vide. Il doit donc rester une vingtaine de kilogrammes de carburant : je vous laisse faire le calcul pour le déterminer. 😉

Limiter le nombre de G

On a vu comment calculer le rapport poussée sur poids d’une fusée à partir de sa masse et de la poussée de ses moteurs maximale. Maintenant, on va s’intéresser à fixer la valeur de RPP maximale atteinte en limitant la poussée des moteurs. Cela peut être utile lorsque l’on souhaite transporter des charges utiles peu résistantes aux fortes accélérations, comme des touristes.

Décidons d’autoriser un RPP maximal de $5$, ce qui correspondra à une accélération maximale de $5\ g$. On va donc chercher une valeur $\alpha$ entre $0$ et $1$ qui nous indiquera la limite à appliquer aux moteurs pour garantir le respect de cette limite.

On cherche à limiter le RPP maximal donc on considère la masse minimale atteignable, c’est-à-dire $7180\ \mathrm{kg}$, et la poussée maximale dans le vide, c’est-à-dire $650000\ \mathrm{N}$. On obtient ainsi l’équation :
$$
\mathrm{RPP_{max}} = 5 = \frac{650000 \alpha}{7180 \cdot 9.81}
$$

On peut en déduire l’équation équivalente en multipliant par le dénominateur et en divisant par $650000$ :
$$
\alpha = \frac{5 \cdot 7180 \cdot 9.81}{650000} \approx 0.5418
$$

On doit donc limiter le moteur à $54 \%$ de sa puissance maximale pour garantir que le vaisseau n’expérimentera pas de poussée supérieure à $5\ g$ lors de son ascension. Je vous laisse essayer par vous même ce réglage et faire profiter des voyages à vos touristes en toute sécurité. 🙂

Conclusion

Dans cette article, on a vu le principe de base de la poussée, son lien avec l’accélération des fusées, $g$ comme unité d’accélération et la notion de rapport poussée sur poids.

On a également vu que l’on pouvait calculer ce RPP en fonctions de la poussée des moteurs et de la masse du vaisseau ou encore calculer la limite à appliquer sur la poussée du moteur pour garantir que le vaisseau n’accélérera pas trop fort.

J’espère que vous avez apprécié la lecture de cet article et que cela vous donnera envie de poursuivre avec d’autres articles disponibles sur le site.

https://fr.wikipedia.org/wiki/Lois_du_mouvement_de_Newton#Troisi%C3%A8me_loi_de_Newton_ou_principe_d’action-r%C3%A9action
Il faut vous y habituer : les scientifiques n’ont pas souvent d’imagination pour donner des noms.
https://fr.wikipedia.org/wiki/Moteur-fus%C3%A9e
En anglais, on parle de « thrust », cf. https://en.wikipedia.org/wiki/Thrust
https://fr.wikipedia.org/wiki/Newton_(unit%C3%A9)
On néglige les frottements de l’air pour des soucis de simplicité et parce que la fusée a alors une vitesse extrêmement faible, ce qui implique des forces de frottements négligeables par rapport aux autres forces.
On vous a déjà prévenu : aucune imagination pour donner des noms originaux mais au moins, on sait de quoi on parle.
En anglais, on parle de « thrust-to-weight ratio » abbrégé en « TWR ».
Principe d’équivalence d’Albert Einstein : https://fr.wikipedia.org/wiki/Principe_d%27%C3%A9quivalence#Le_principe_d’%C3%A9quivalence_d’Albert_Einstein
Je vous le promets : on en parlera dans un futur article 🙂

KSC

KSC